Daten-Durchblick

In meinem zweiten Semester trete ich in ein Modul ein, das die Sprache der Daten erlernbar macht: Quantitative Methoden der Informatik. Hier geht es nicht um abstrakte Algorithmen allein, sondern um den gesamten Weg – von der ersten Fragestellung bis zur fundierten Entscheidung auf Basis von Zahlen und Fakten.

Was bedeutet das konkret?
Wir lernen, wie man Daten systematisch erhebt und strukturiert, welche Skalenniveaus zu beachten sind und wie sich mit Explorativer Datenanalyse und deskriptiver Statistik erste Muster entdecken lassen. Anschließend vertiefen wir uns in inferenzstatistische Verfahren, um Zusammenhänge mathematisch zu modellieren und Hypothesen zu testen.

Dieses Fundamentwissen ist mehr als nur eine akademische Pflichtübung: Es bildet das Sprungbrett in die Welt der Künstlichen Intelligenz und des Data Science. Wer hier die Prinzipien von Datenerhebung, Gütekriterien und Modellierung verinnerlicht, verfügt über das Rüstzeug, um in Forschung, Wirtschaft oder Softwareentwicklung datengetriebene Innovationen voranzutreiben.

Nun aber genug Allgemeines Geschwafel darüber was sich hinter diesem Thema verbirgt, denn ich befinde mich gerade in der Vorbereitung auf die bevorstehende Modulprüfung und möchte euch die Gelegenheit geben mit in diese Welt einzutauchen.

Vom Allgemeinen ins Spezielle, so sind die Vorlesungen in der Regel auch aufgebaut, was es mir etwas leichter macht euch dieses Thema etwas näher zu bringen.

Damit man mit Daten umgehen kann, benötigt man zunächst ein Gefühl für Daten.

Wie in dem Modul Cloudtechnologie gelernt:

Unter quantitativen Methoden versteht man statistische Verfahren oder auch Methoden, die auf den Erkenntnissen der Data Literacy aufbauen und zentrale wissenschaftliche Gütekriterien für die Forschung definieren.

Diese wissenschaftlichen Gütekriterien sind:

• Ethische Aspekte: Das Abwägen potenziell schädlicher Konsequenzen welche durch die Auswertung von Daten in einem gewissen Zusammenhang durch zum Beispiel eine Studie entstehen können.
• Objektivität: Gewährleisten, dass die Resultate unabhängig von den Personen sind, die die Untersuchung durchführen.
• Transparenz: Das empirische Vorgehen bei der Erfassung der Daten, Entscheidungen lückenlos zu dokumentieren, so dass diese Nachvollziehbar sind.
• Reliabilität: Messverfahren so zu gestalten, dass sie bei Wiederholung konsistente und reproduzierbare d.h. zuverlässige Ergebnisse liefern.
• Interne Validität: Sicherstellen das kausale Schlussfolgerungen korrekt sind, etwa zu klären, ob zum Beispiel ein Medikament wirklich die Genesung herbeiführt oder ob andere Einflüsse im Spiel sind.
• Externe Validität: Zu Prüfen, inwieweit Befunde auf andere Gruppen oder Situationen übertragbar sind z. B., ob Erkenntnisse von Tier-Experimenten auf den Menschen anwendbar sind. 
• Genauigkeit: Erreichen einer hohen Messpräzision, sodass systematische Abweichungen minimiert werden.

Hieraus resultiert, dass ein

Messergebnis = Wert der Eigenschaft + Systematische Abweichung + Zufällige Schwankung

ist.

Es ergeben sich aus dem Mix valide und reliabel diese Vier Modelle A, B, C und D, wovon in der Wissenschaft versucht wird immer ein reliables und valides Ergebnis aus den Daten zu erhalten.

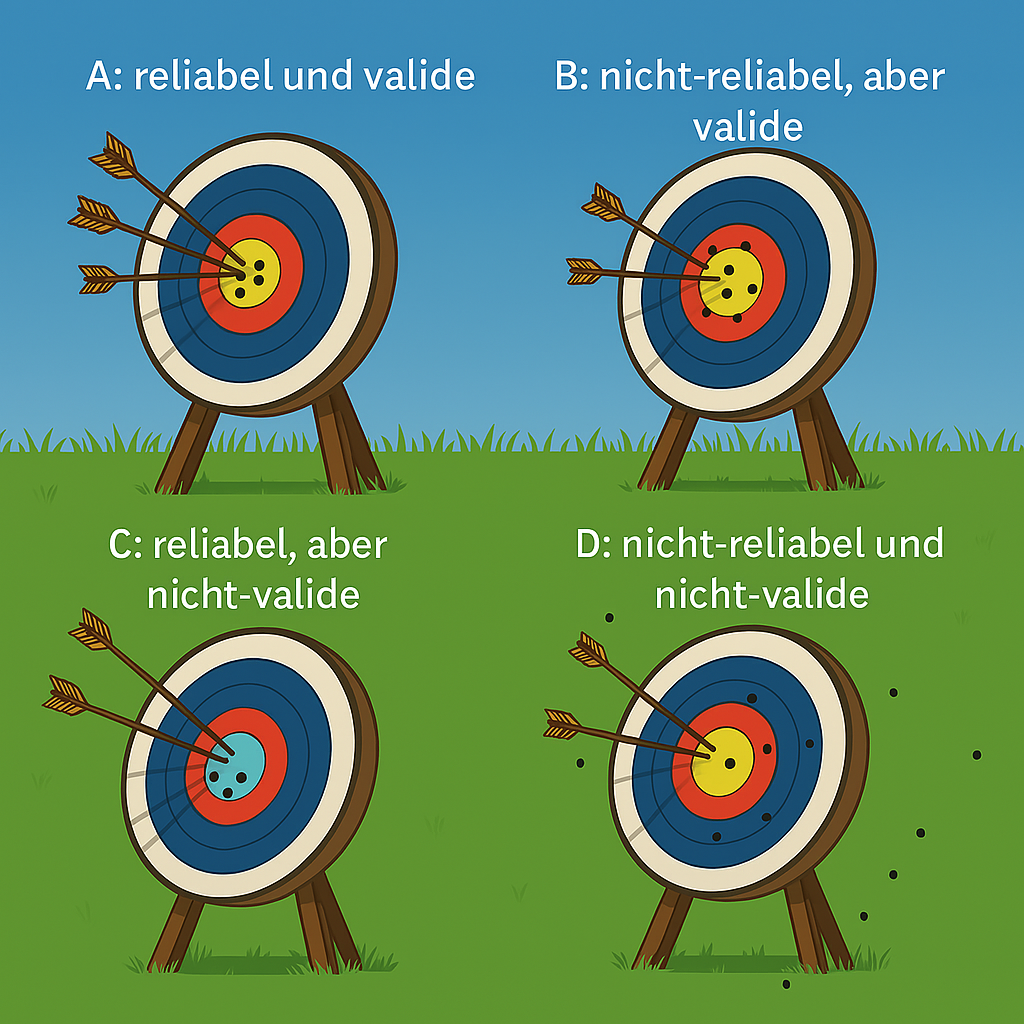
Vorsicht: Daten welche reliabel, aber nicht-valide sind, könnten den Anschein erwecken, dass Sie in einem Zusammenhang stehen, sind es aber nicht, wenn die Schlussfolgerung falsch ist, jedoch korrekt gemessen wurde.

Daten, die anhand von Variablen (Attributen) erfasst und in ihrer Rohform vorliegen, weisen unterschiedliche Skalenniveaus auf. Diese legen fest, welche Vergleiche zulässig sind und welche statistischen Verfahren angewendet werden können. Klassisch unterscheidet man vier Skalenniveaus: nominal, ordinal, intervall- und verhältnisskaliert. Darüber hinaus unterscheidet man diskrete und latente Variablen.

Variablentypen im Überblick

• Kategorial nominal
  Merkmale, die in unveränderliche Kategorien fallen, ohne jegliche Reihenfolge. Beispiele: Geschlecht (m/w), Blutgruppen (A, B, AB, 0).

• Kategorial ordinal
  Kategorien mit einer klaren Rangfolge, bei der Abstände aber nicht quantifiziert werden können. Beispiele: Schulnoten (1 bis 6), Zufriedenheitsrankings (niedrig bis hoch).

• Intervallskaliert
  Messwerte mit gleich großen Abständen, aber ohne echten Nullpunkt. Temperatur in °C ist typisch: Der Abstand zwischen 10 °C und 20 °C ist gleich, aber ein Wert von 0 °C bedeutet nicht „kein Wärmegrad“.

• Verhältnisskaliert
  Wie Intervall, jedoch mit absolutem Nullpunkt. Hier sind alle arithmetischen Operationen erlaubt, auch Quotienten. Beispiele: Körpergröße in cm, Gewicht in kg.

• Diskret
  Abzählbare Messwerte, die meist nur ganze Zahlen annehmen. Anzahl Kinder oder Würfelergebnisse können nicht in Bruchteilen auftreten.

• Latent
  Nicht direkt beobachtbare Merkmale, die erst durch Indikatoren operationalisiert werden müssen. Beispiele: Intelligenz, Motivation oder „Interesse an Statistik“.

Nachdem wir die Skalenniveaus und Variablentypen abschließend geklärt haben, wenden wir uns nun der Modellierung zu. Ein Modell ist eine bewusste Vereinfachung der realen Welt, bei der nur diejenigen Aspekte eingebracht werden, die für unsere Fragestellung relevant sind. Anhand von Daten können solche Modelle

• entwickelt (Modellspezifikation),
• geprüft (Gütekriterien, Fit-Maße)
• und schließlich zur Vorhersage neuer Beobachtungen verwendet werden.

Grundbausteine eines Modells

Stellen wir uns folgende Forschungsfrage vor: Verbessert der Konsum von Bio-Lebensmitteln die Lebenserwartung?

• Abhängige Variable (Zielgröße)
  y = Lebenserwartung in Jahren
• Unabhängige Variable (Prädiktor)
  x = Indikator für Bio-Konsum (Ja / Nein)
• Kovariable
  z = Geschlecht (männlich / weiblich), um einen möglichen Einfluss darauf zu kontrollieren
• Rest (Fehlerterm)
  ε = alle unbeobachteten Einflüsse, die nicht im Modell erfasst sind

Die modelltheoretische Grundform lautet dann:

y = f(x, z) + ε

Im einfachsten Fall betrachten wir eine lineare Beziehung:

y = β₀ + β₁·x + β₂·z + ε

Hier beschreiben die Parameter β₀, β₁ und β₂ den Einfluss der jeweiligen Variablen, während ε die zufällige Abweichung (“Rauschen”) zusammenfasst.

Population vs. Stichprobe: Griechisch und Lateinisch

Bei der Datenerhebung und -auswertung unterscheiden wir sprachlich zwischen:

• Griechischen Buchstaben (β, σ, μ …), die Parameter in der Population kennzeichnen
• Lateinischen Buchstaben (b, s, x̄ …), die Statistiken in unserer Stichprobe darstellen

Beispiel:
β₁ ist der wahre, unbekannte Effekt des Bio-Konsums auf die Lebenserwartung in der Gesamtpopulation.
b₁ ist der auf Basis der vorliegenden Stichprobe geschätzte Wert für β₁.

Dieser Notationsunterschied hilft uns, klar zwischen dem Idealzustand (Population) und der Realität unserer Daten (Stichprobe) zu trennen.

Nachdem wir Population und Stichprobe voneinander abgegrenzt haben, wenden wir uns nun den unterschiedlichen Stichprobenverfahren und Studiendesigns zu, die den Rahmen für eine valide und zuverlässige Datenerhebung bilden.

Stichprobenverfahren

• Zufällige Stichprobe
  Jedes Element der Zielpopulation hat dieselbe Chance, ausgewählt zu werden.
  → Die Ergebnisse lassen sich – bei Unsicherheit durch Rauschen – auf die Gesamtpopulation verallgemeinern. Systematische Verzerrungen sind ausgeschlossen.

• Gelegenheitsstichprobe
  Es werden diejenigen Elemente ausgewählt, die leicht verfügbar sind.
  → Das Ergebnis kann verzerrt sein. Sowohl systematisches Bias als auch Rauschen können vorliegen, sodass kein valider Rückschluss auf die Population möglich ist.

• Vollerhebung
  Alle Beobachtungseinheiten der Population werden erfasst.
  → Parameter und Statistik sind identisch, Verzerrung entsteht nur durch Messfehler oder Ausfälle.

Studiendesigns

• Beobachtungsstudie
  Daten zu unabhängiger Variable x und abhängiger Variable y werden lediglich erhoben, ohne Eingriff in das Geschehen.
  → Kausalitäten lassen sich nur eingeschränkt prüfen, da Confounding-Faktoren unkontrolliert bleiben können.

• Randomisiertes Experiment
  Die unabhängige Variable x wird aktiv und zufällig variiert (z. B. Zuweisung unterschiedlicher Lernumgebungen). Anschließend wird das Ergebnis y gemessen.
  → Führt zu hoher interner Validität, da Störfaktoren gleichverteilt werden und systematische Verzerrungen minimiert sind.